Integer benchmarks

In these benchmarks, integer is compared to the following types:

• the builtin std::int64_t and std::uint64_t types,

• the 128-bit integral types __int128_t and __uint128_t, available on GCC and Clang,

• the cpp_int class from the Boost.Multiprecision library. Similarly to integer, cpp_int is a signed multiprecision integer class which uses a small-value optimisation;

• the gmp_int GMP wrapper from the Boost.Multiprecision library. gmp_int is a wrapper around the mpz_t type from the GMP library. In the benchmarks, the gmp_int API is used only for ease of initialisation and destruction of GMP objects: all arithmetic operations are implemented by calling directly the GMP API, and thus we regard the performance of gmp_int as a proxy for the performance of mpz_t;

• the fmpzxx class from the FLINT library. Similarly to integer, fmpzxx is a signed multiprecision integer class which uses a small-value optimisation.

In all benchmarks, a lower runtime is better.

Dot product

This benchmark measures the time needed to compute the dot product of two integer vectors of size \(3\times 10^7\) containing randomly-generated values. Multiply-add primitives (if available) are used for the accumulation of the dot product.

1-limb unsigned integers

In this setup, the integer vectors are initialised with small non-negative values, and the final dot product is less than \(2^{64}\). mp++ integers with 1 limb of static size are employed.

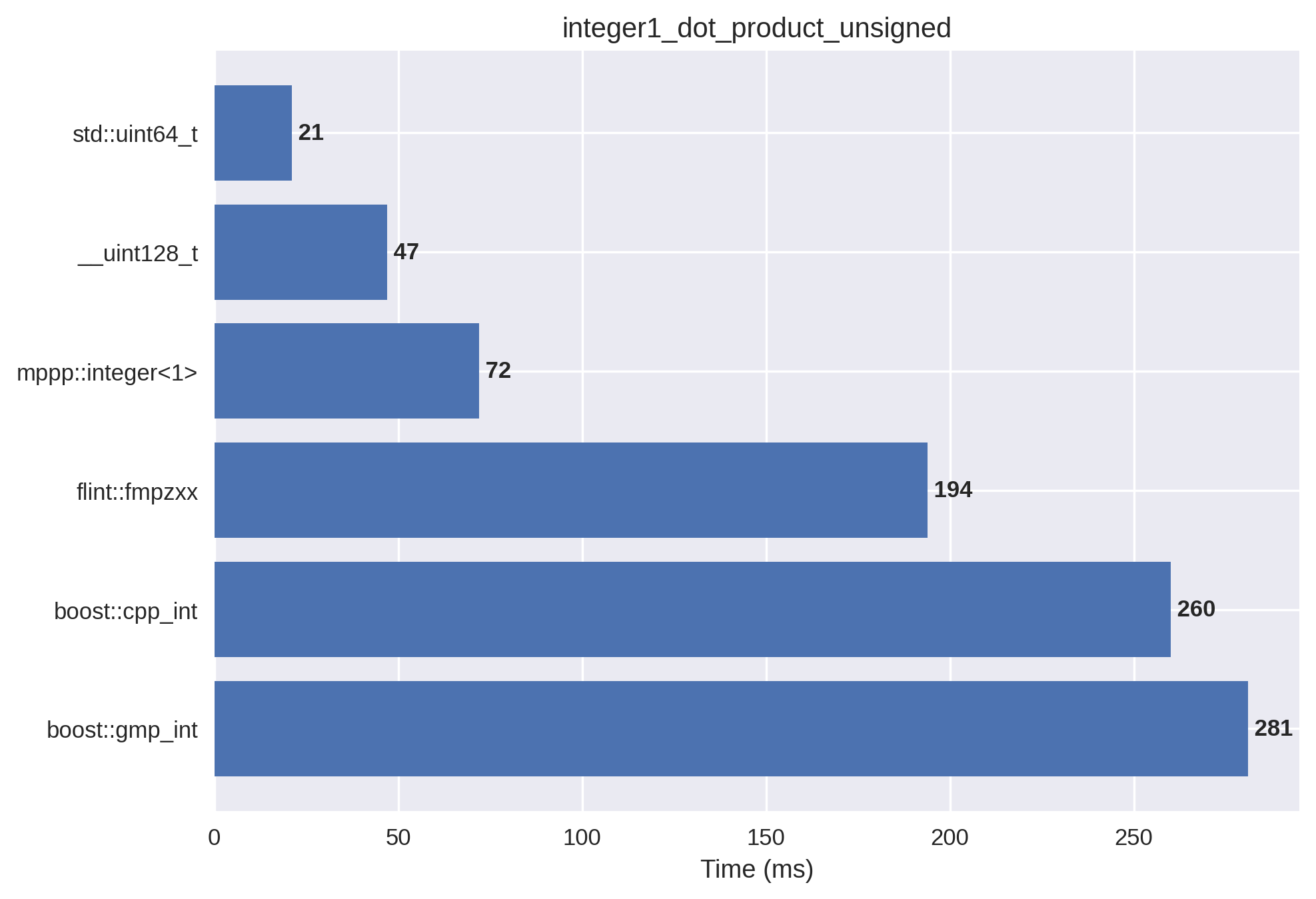
In this particular benchmark, mp++ is almost 4 times faster than GMP. mp++ is also faster than cpp_int and FLINT, albeit by a smaller margin. With respect to the 64/128-bit builtin integer types, there are x4/x2 slowdowns.

1-limb signed integers

This setup is almost identical to the previous one, but this time the vectors are initialised with both positive and negative values.

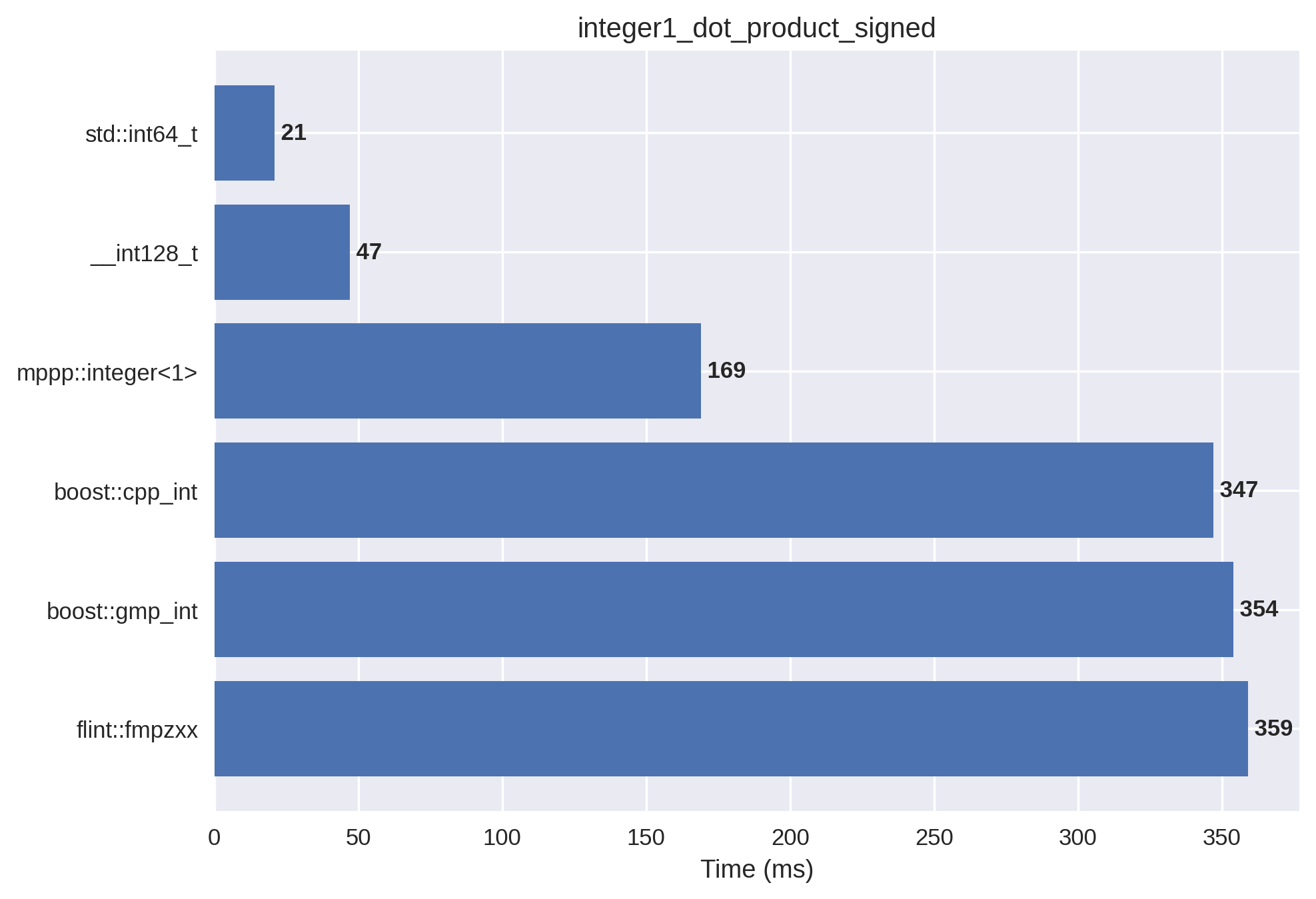
The presence of both positive and negative values has a noticeable performance impact with respect to the previous test for all multiprecision libraries. This is due to the fact that sign handling in multiprecision computations is typically implemented with branches, and when positive and negative values are equally likely the effectiveness of the CPU’s branch predictor is much reduced.

The performance advantage of mp++ with respect to the other libraries is retained, albeit by a smaller margin. With respect to the 64/128-bit builtin integer types, there are x8/x4 slowdowns.

2-limb unsigned integers

This setup is the 2-limb version of the 1-limb unsigned benchmark: the vectors are initialised with larger non-negative values, the final result is less than \(2^{128}\), and mp++ integers with 2 limbs of static size are now employed.

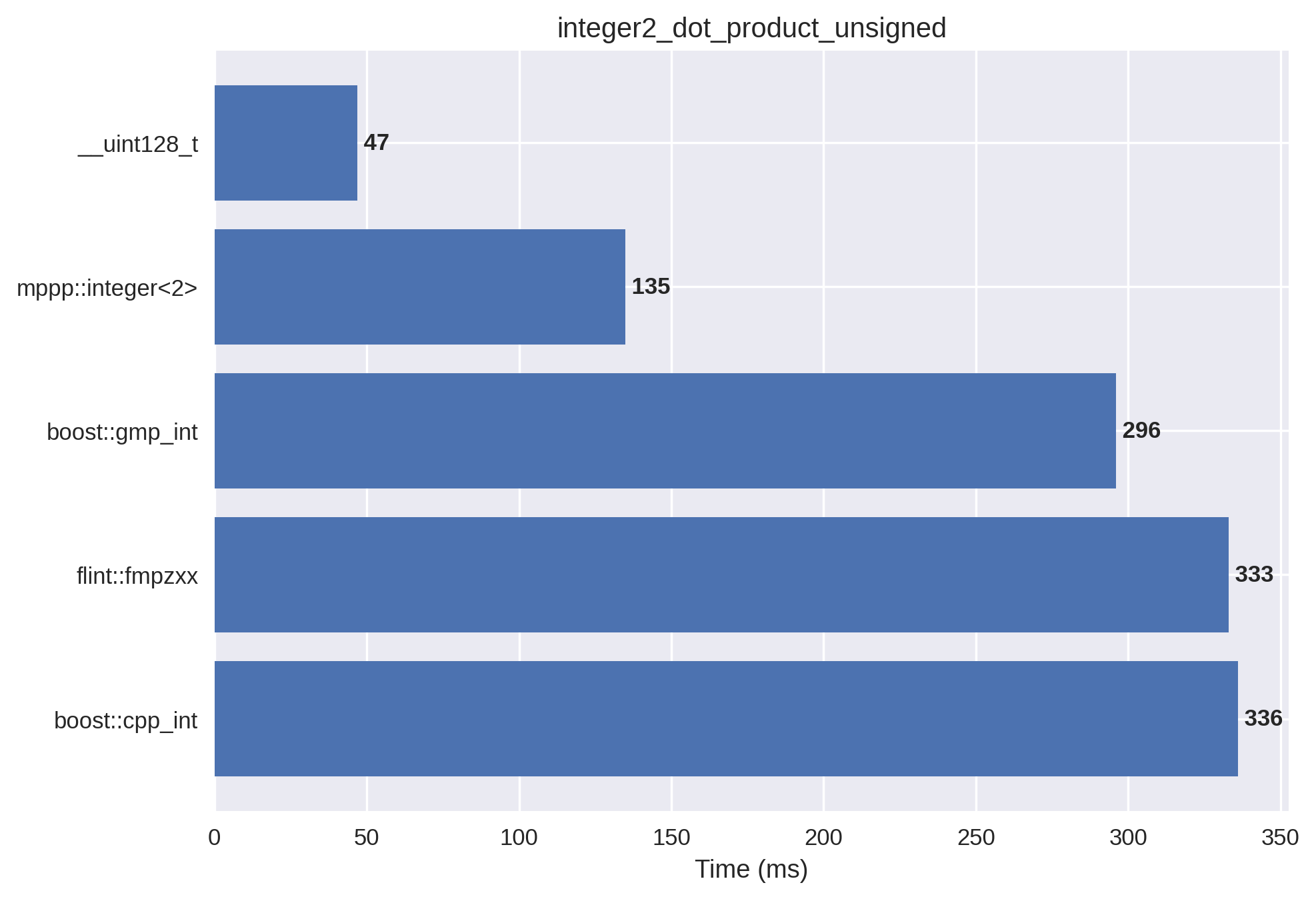
The benchmark shows that mp++’s specialised arithmetic functions pay off in terms of raw performance in this scenario.

2-limb signed integers

This setup is the signed version of the previous benchmark.

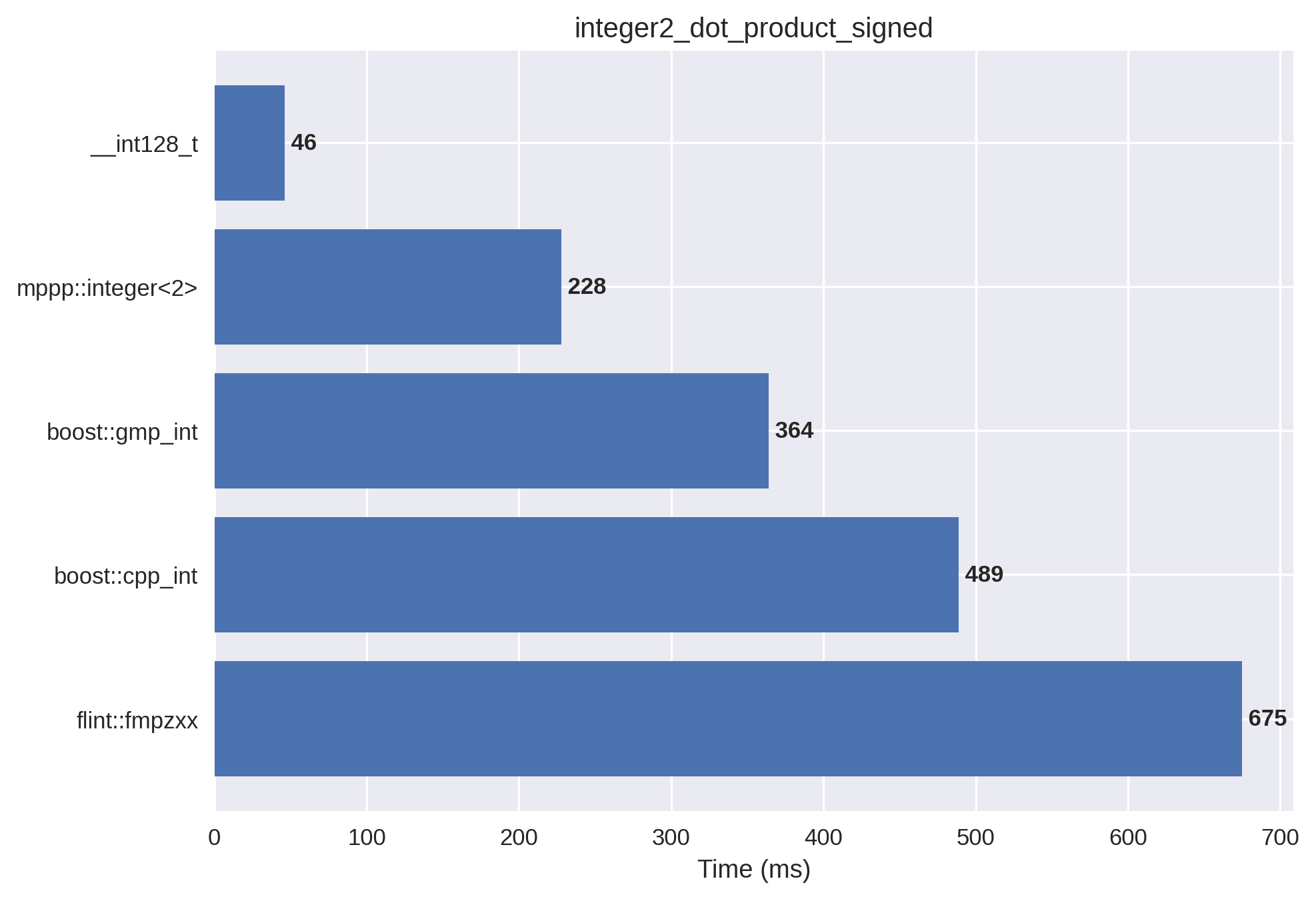
As explained earlier, arithmetic with mixed positive and negative values is more expensive than arithmetic with only non-negative values.

Vector multiply-add

In this benchmark, we first compute the element-wise multiplication of two random vectors of size \(3\times 10^7\), followed by the addition to another random vector of the same size. This workload allows to measure the efficiency of the multiplication and addition operations (whereas in the dot product benchmark the multiply-add primitives were employed), and it also increases the pressure on the memory subsystem (due to the need to write into large vectors instead of accumulating the result into a single scalar).

1-limb unsigned integers

In this setup, the integer vectors are initialised with small non-negative values. mp++ integers with 1 limb of static size are employed.

This time mp++ is more than 7 times faster than GMP, while still maintaining a performance advantage over cpp_int and FLINT. The slowdown with respect to 64-bit integers is less than x3, while mp++ performs similarly to 128-bit integers for this particular test.

1-limb signed integers

In this setup, the vectors are initialised with both positive and negative values.

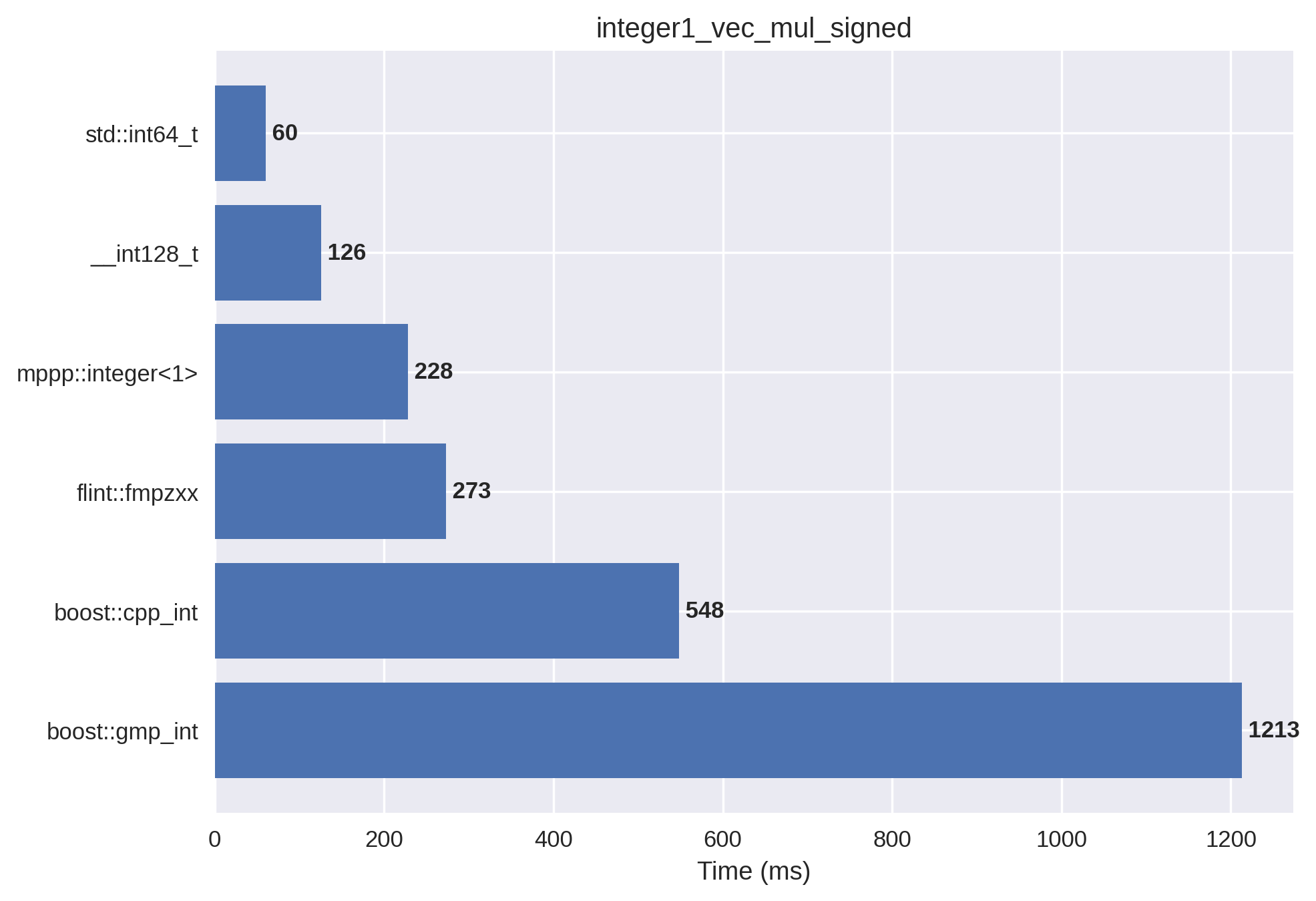
We can see again how the introduction of mixed positive and negative values impacts performance negatively with respect to the unsigned setup. With respect to the 64/128-bit builtin integer types, there are x4/x2 slowdowns.

2-limb unsigned integers

This setup is the 2-limb version of the 1-limb unsigned benchmark: the vectors are initialised with larger non-negative values, and mp++ integers with 2 limbs of static size are now employed.

The benchmark shows again that mp++’s specialised arithmetic functions deliver strong performance.

2-limb signed integers

This setup is the signed version of the previous benchmark.

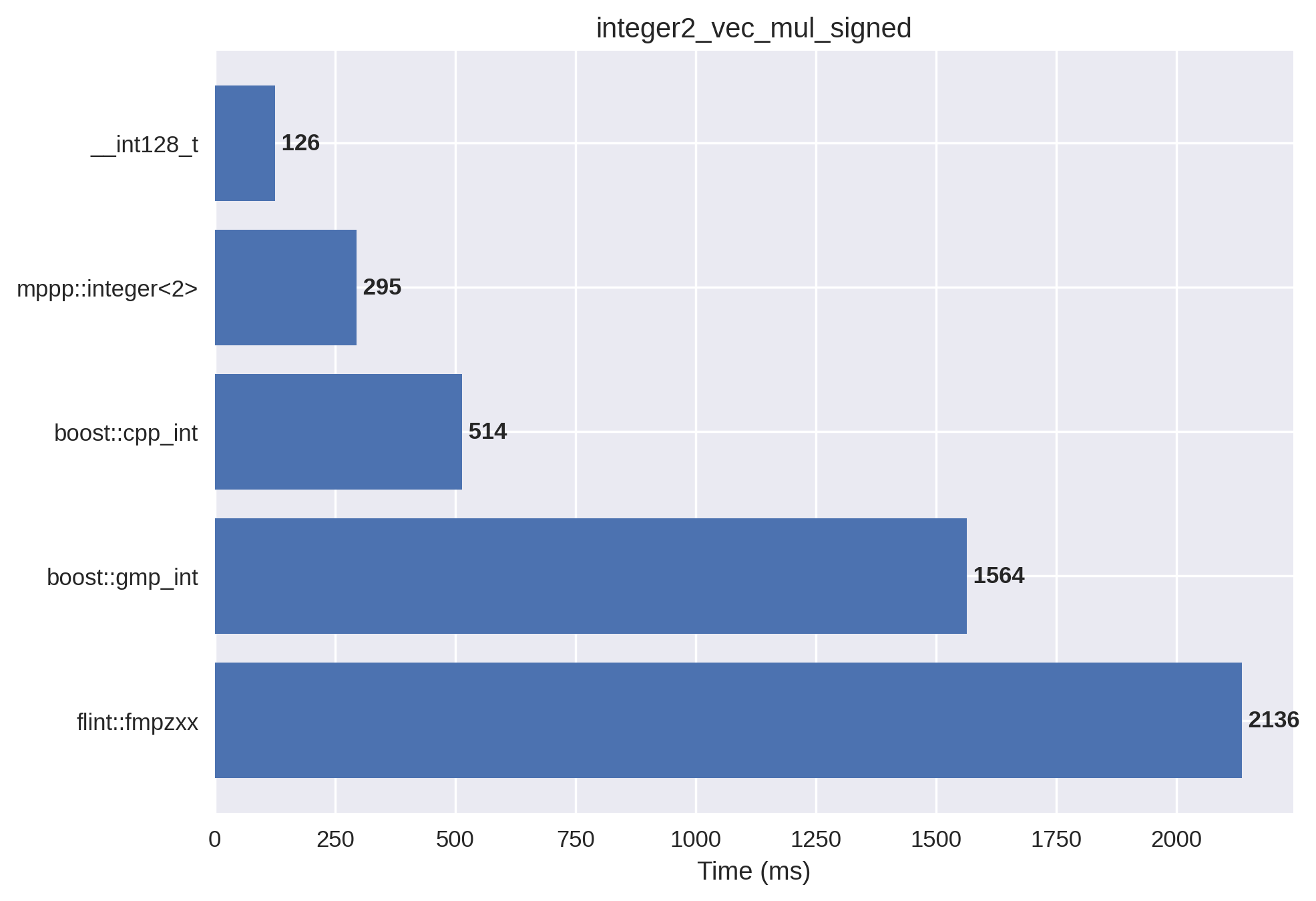
Vector division

In this benchmark we compute the element-wise truncated division of two randomly-generated vectors of size \(3\times 10^7\), followed by the sum of all the values in the quotient vector.

1-limb unsigned integers

In this setup, the integer vectors are initialised with small non-negative values. mp++ integers with 1 limb of static size are employed.

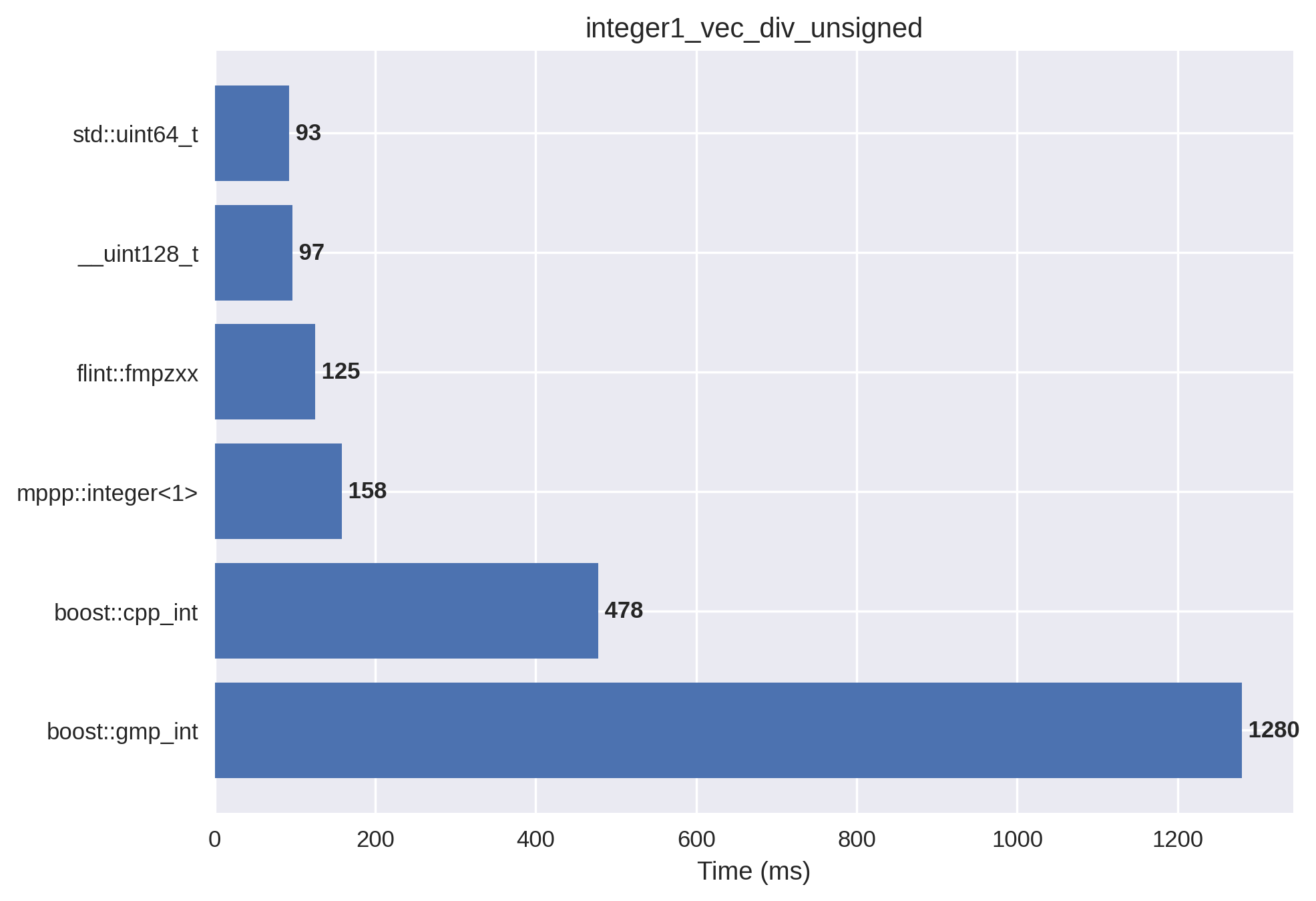
mp++ and FLINT perform well on this test, and they are about 8 times faster than GMP.

1-limb signed integers

In this setup, the vectors are initialised with both positive and negative values.

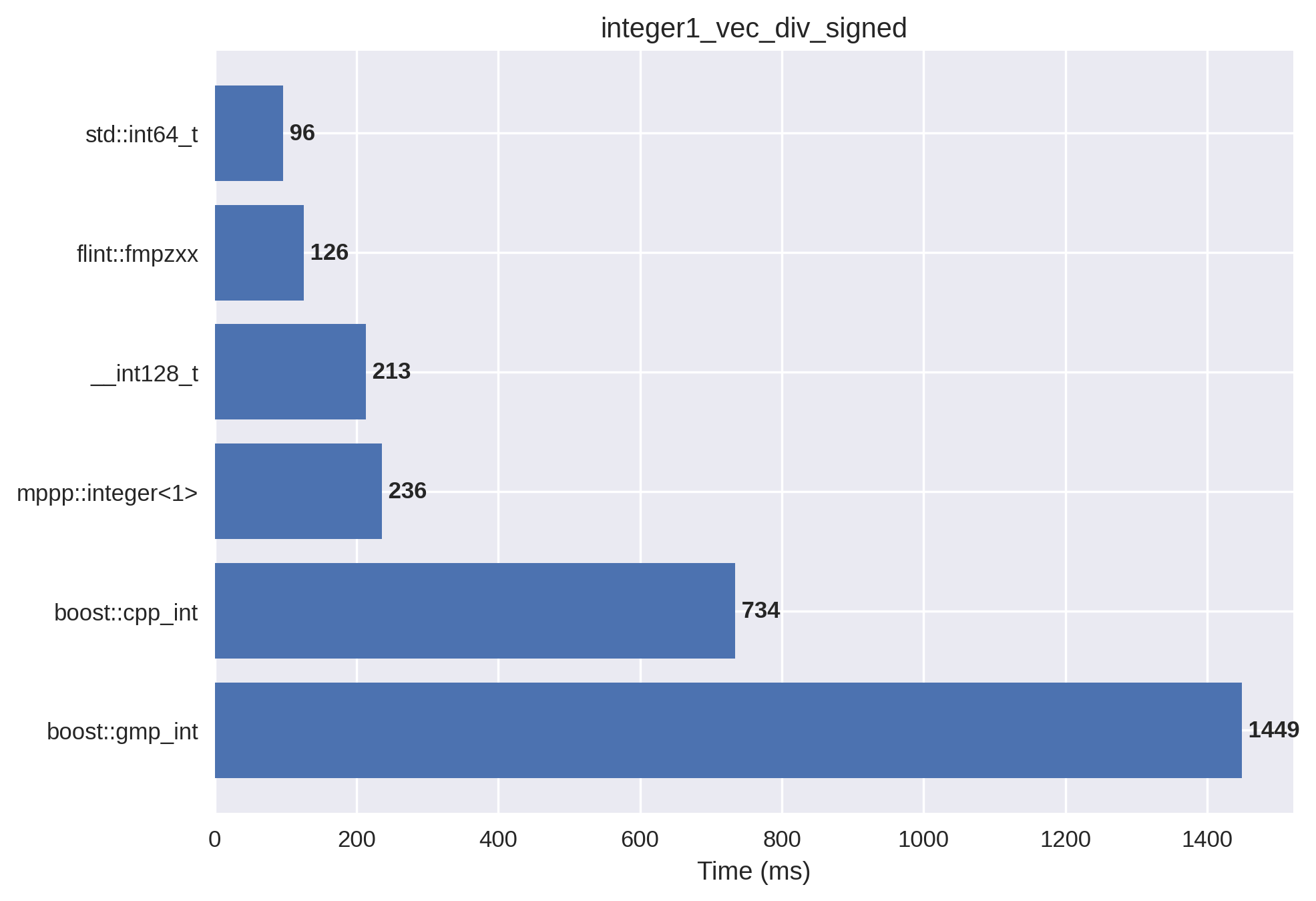
Here we can see FLINT pulling ahead of mp++. FLINT uses a signed integer representation for small values that allows to avoid branching based on the signs of the operands. Coupled to the fact that there’s no need to do overflow checking during division, FLINT’s implementation has a distinct performance advantage in this specific test.

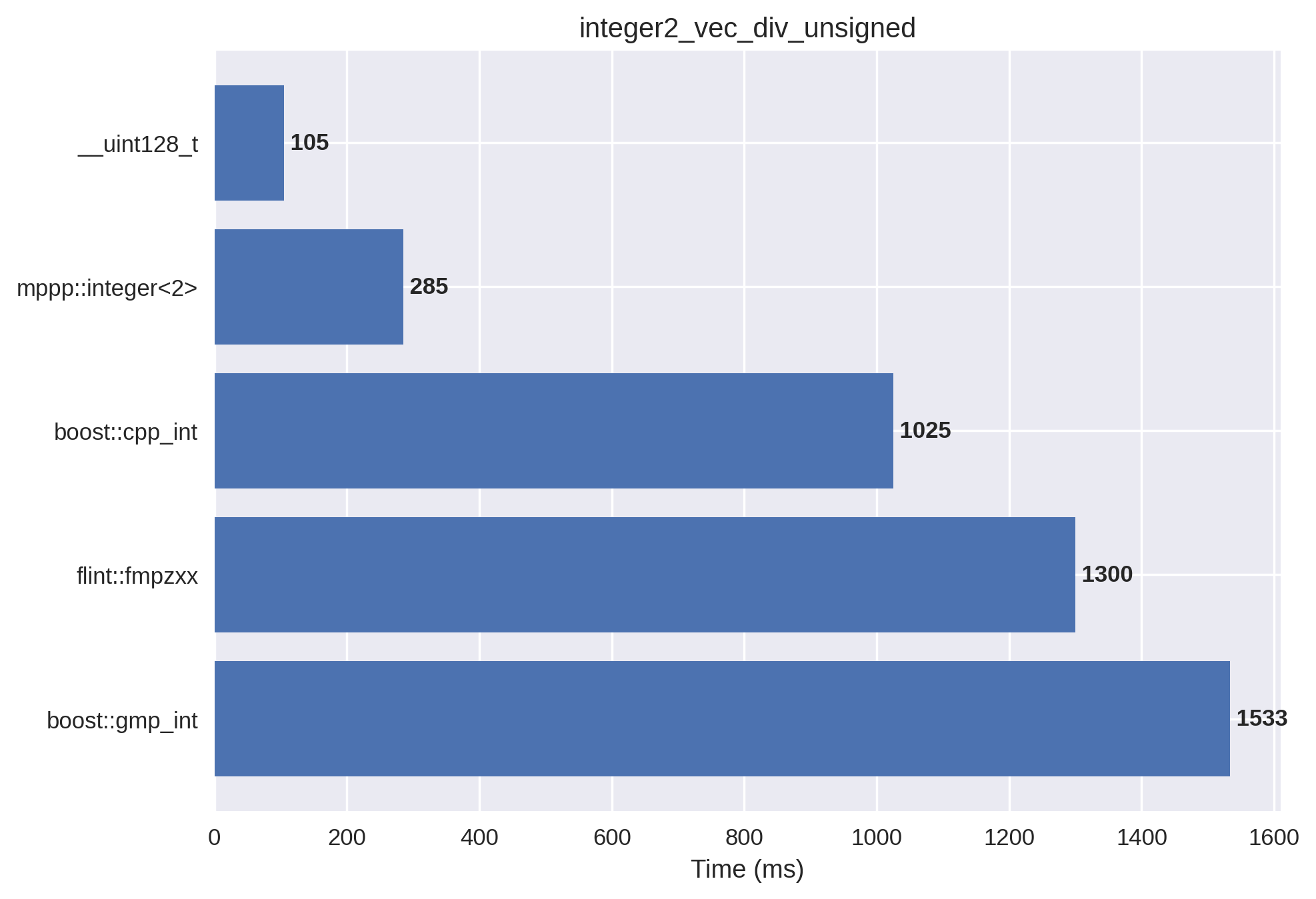
2-limb unsigned integers

This setup is the 2-limb version of the 1-limb unsigned benchmark: the vectors are initialised with larger non-negative values, and mp++ integers with 2 limbs of static size are now employed.

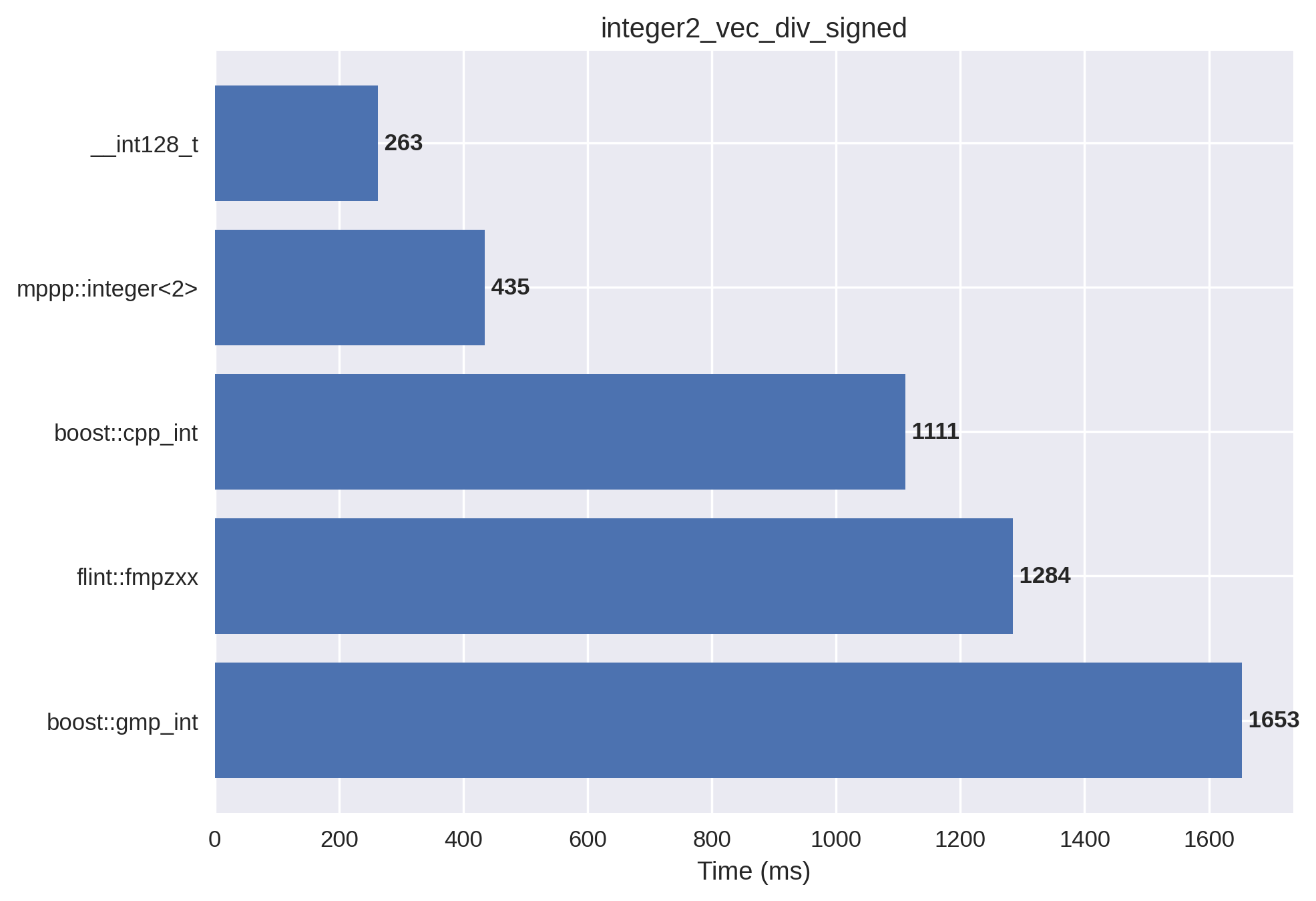
2-limb signed integers

This setup is the signed version of the previous benchmark.

Sorting

This benchmark consists of the sorting (via std::sort()) of a randomly-generated vector of \(3\times 10^7\) integers.

1-limb unsigned integers

In this setup, the integer vector is initialised with small non-negative values. mp++ integers with 1 limb of static size are employed.

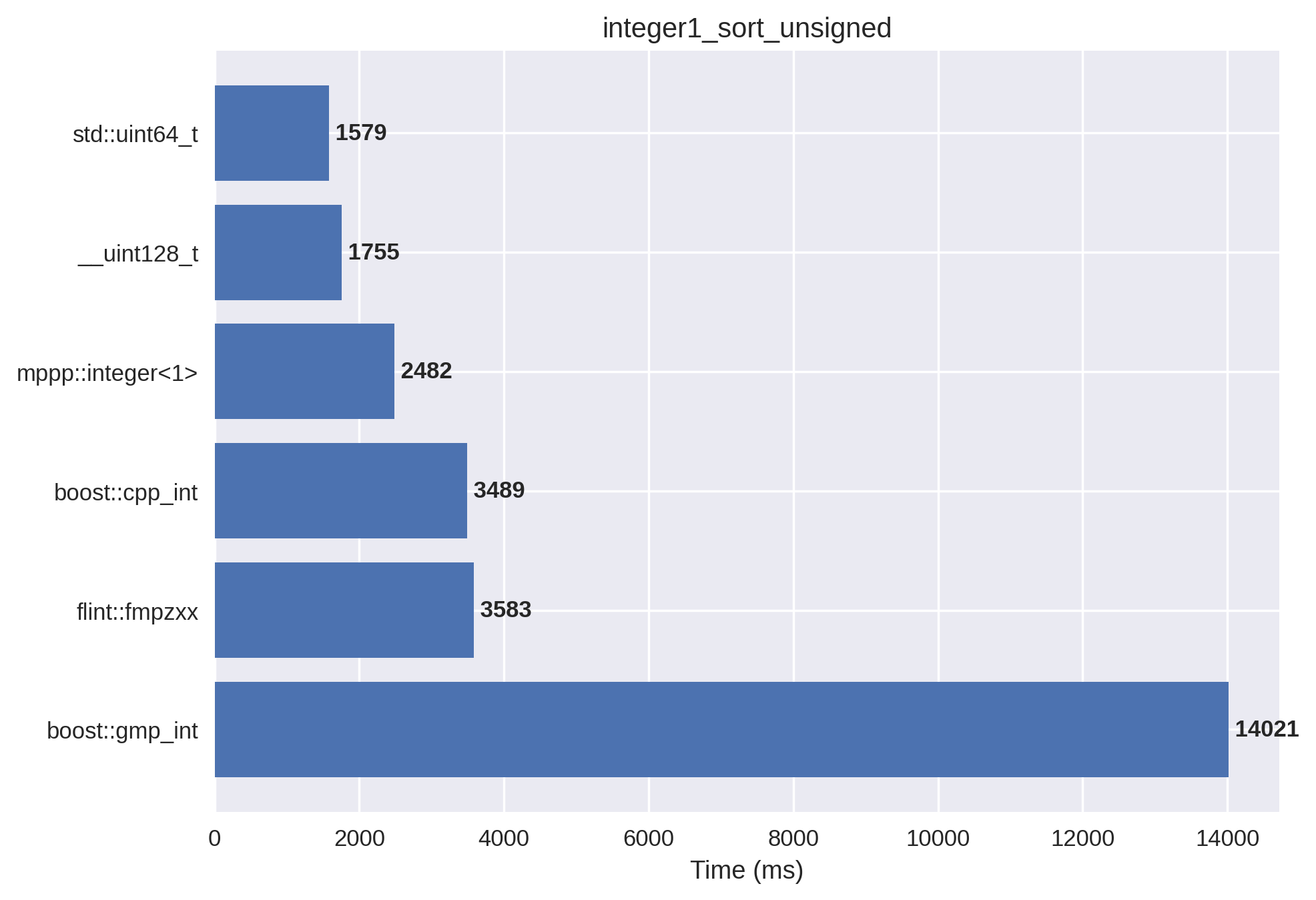
Here again it can be seen how the small-value optimisation implemented in mp++, cpp_int and FLINT pays off on large datasets with respect to plain GMP integers. mp++ shows a modest performance increase with respect to cpp_int and FLINT.

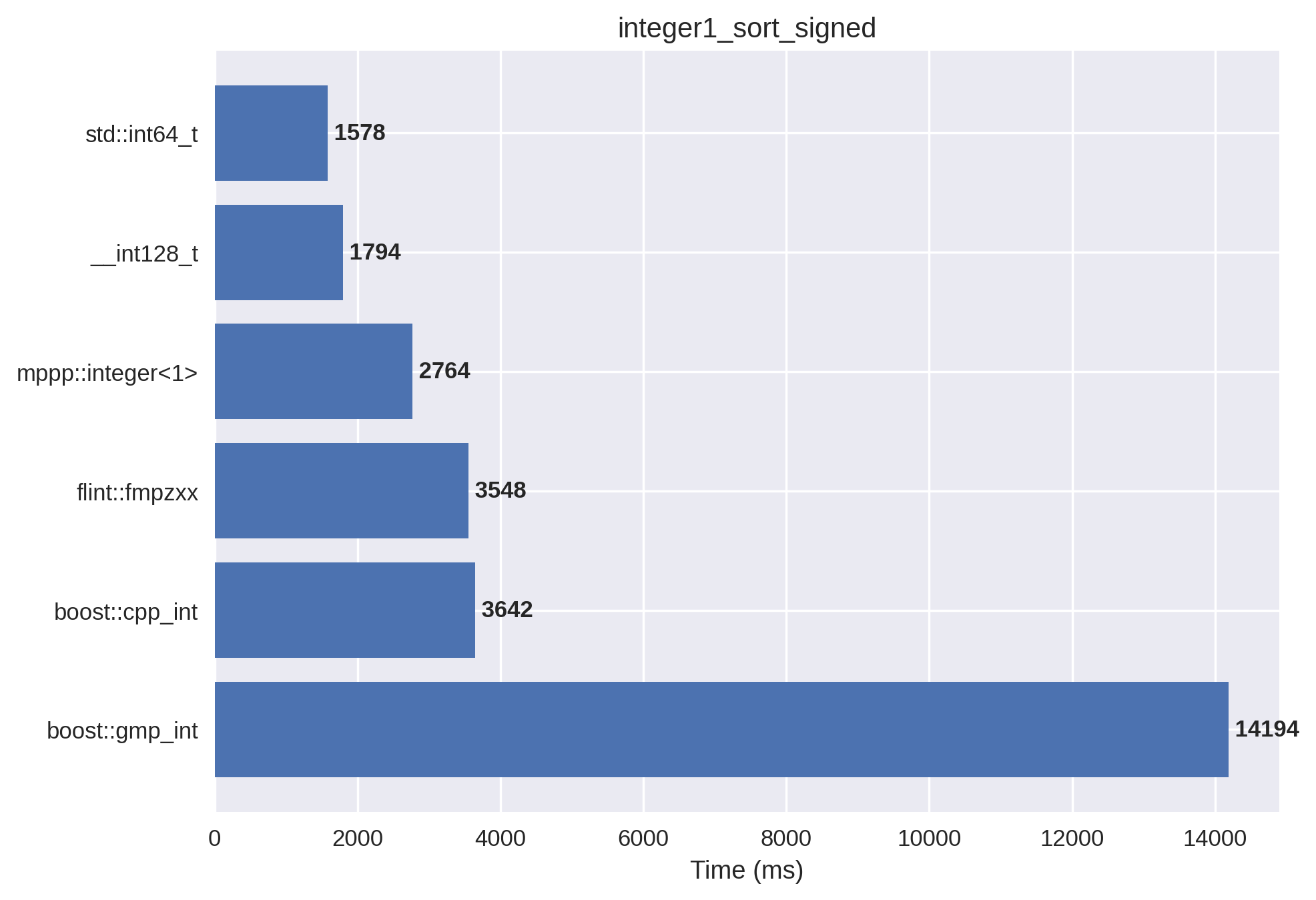
1-limb signed integers

In this setup, the vector is initialised with both positive and negative values.

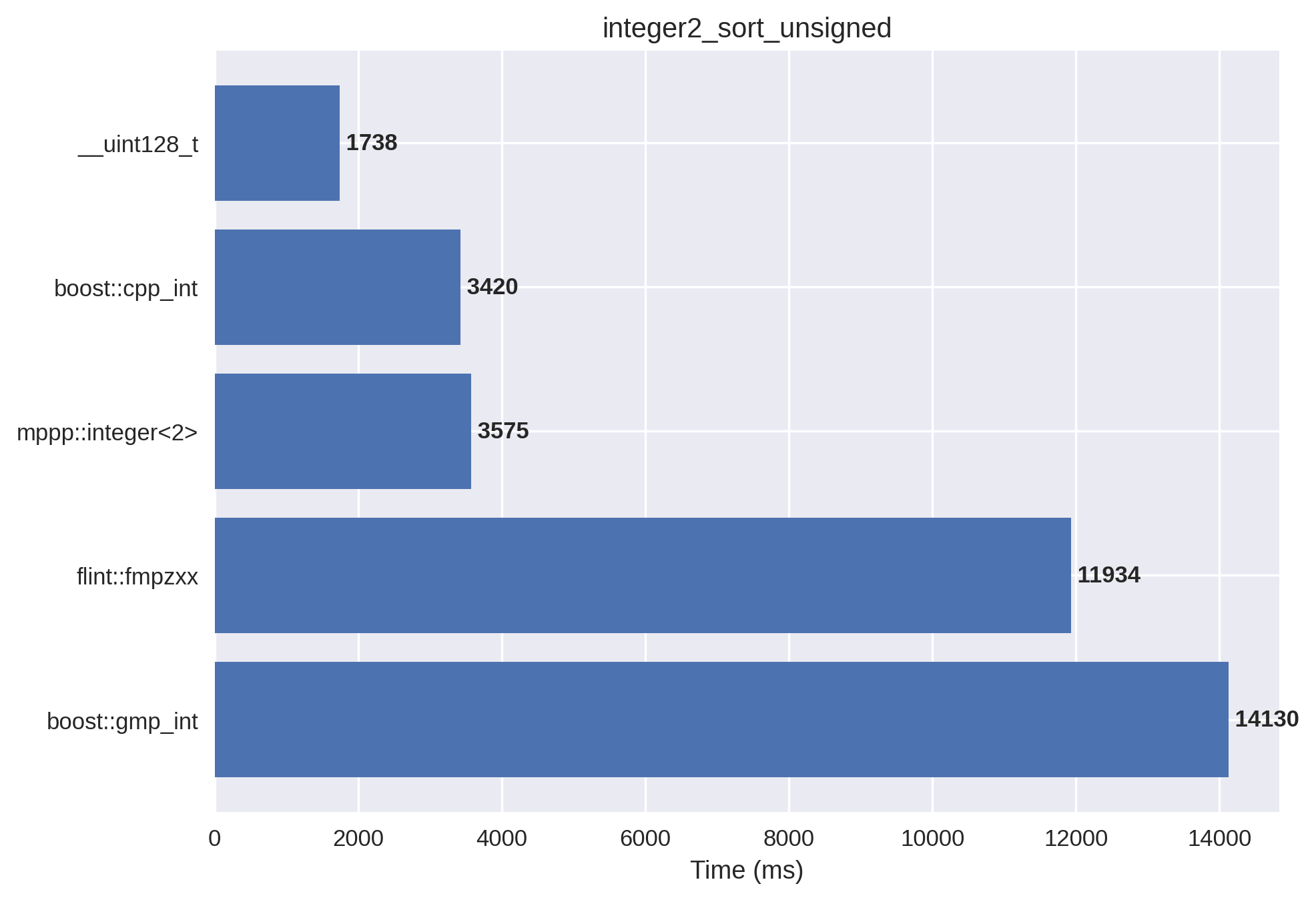
2-limb unsigned integers

In this setup, the integer vector is initialised with non-negative values in the \(\left[2^{64},2^{128}\right)\) range. mp++ integers with 2 limbs of static size are employed.

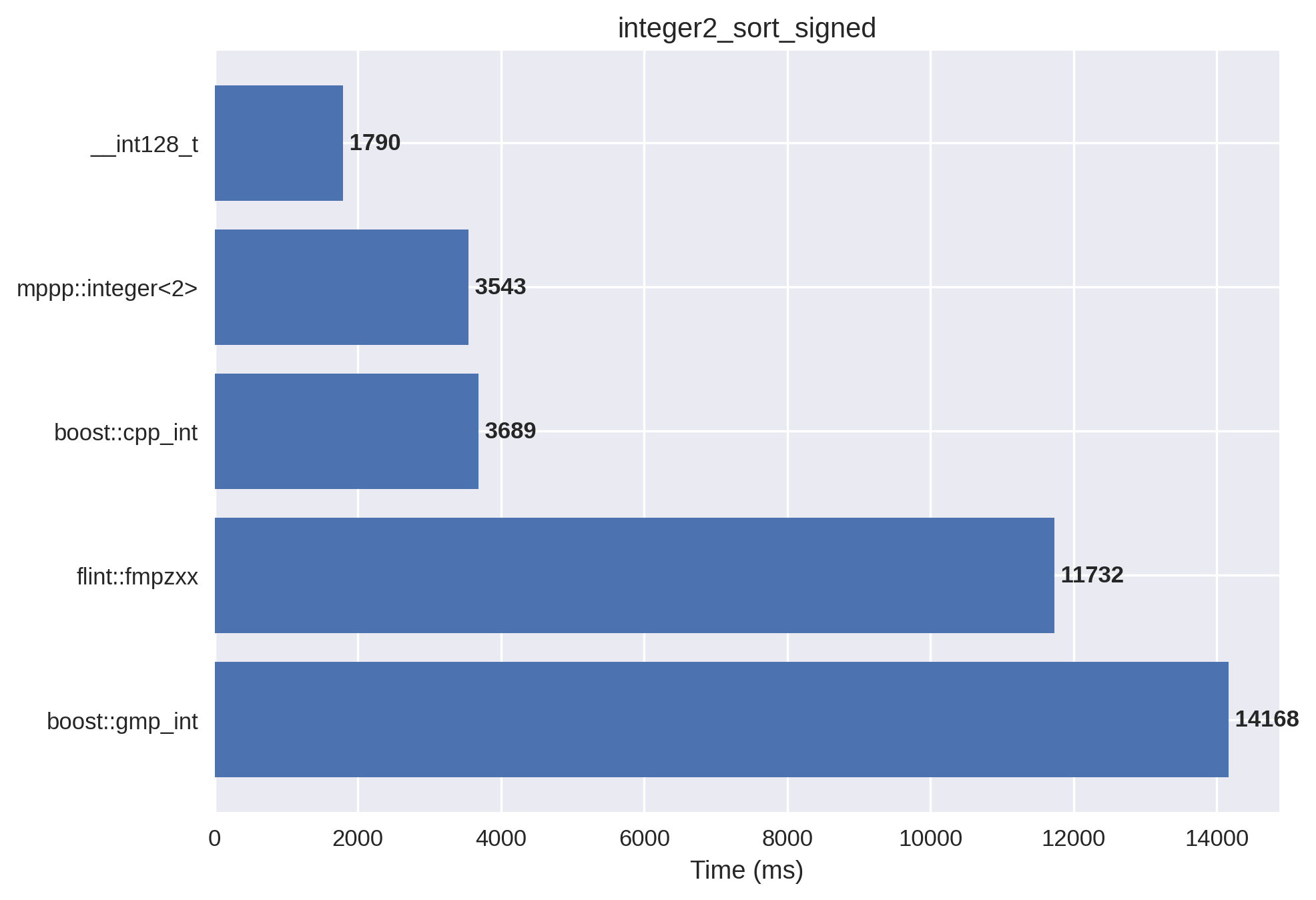
2-limb signed integers

In this setup, the vector is initialised with both positive and negative values in the \(\left(-2^{128},2^{128}\right)\) range. mp++ integers with 2 limbs of static size are employed.

Left bit shift

This benchmark consists of the element-wise left bit shifting of a randomly-generated vector of \(3\times 10^7\) integers.

1-limb unsigned integers

In this setup, the integer vector is initialised with small non-negative values, which are then left bit shifted by a small random amount (so that the result always fits into a machine word). mp++ integers with 1 limb of static size are employed.

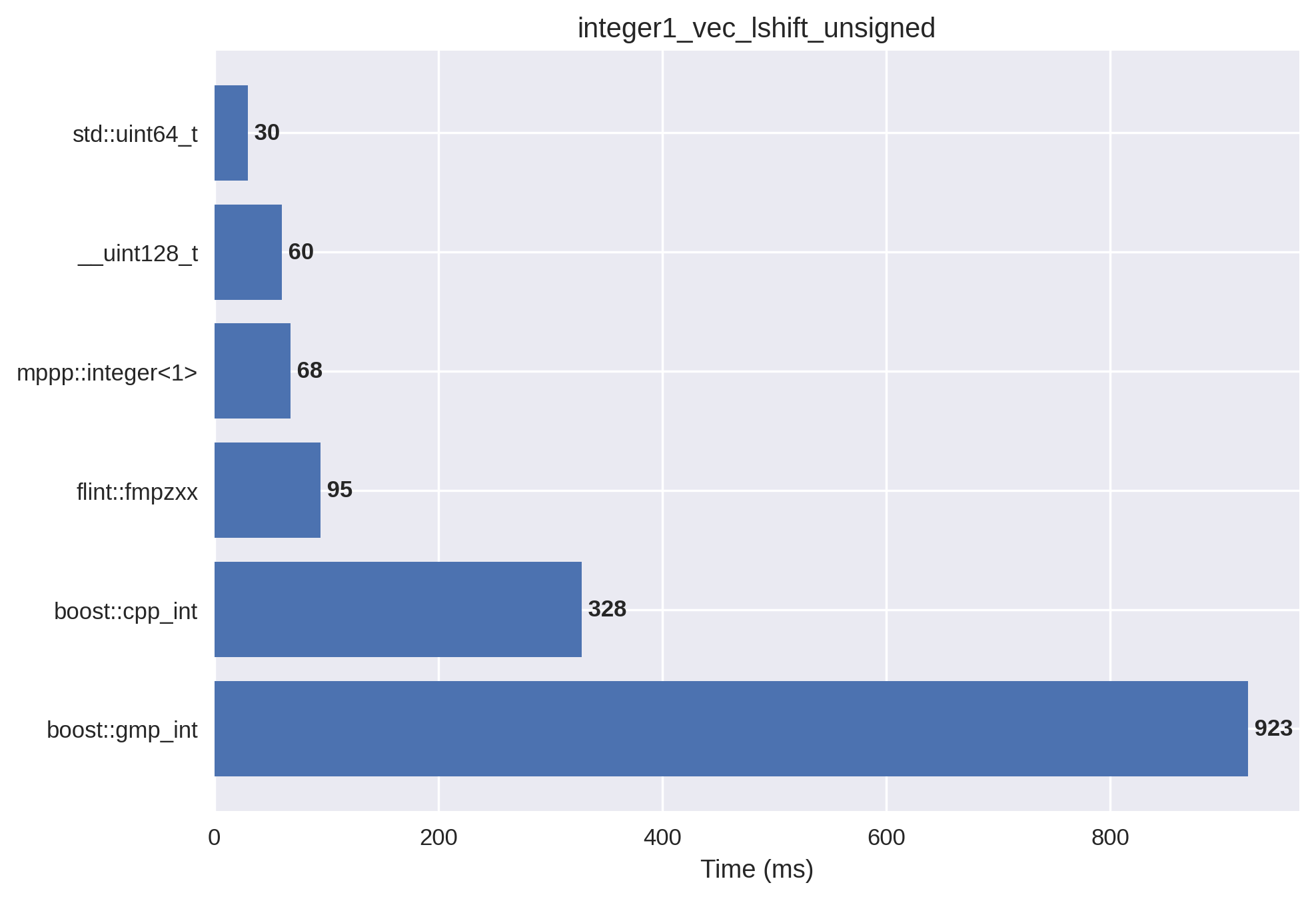
1-limb signed integers

In this setup, the integer vector is initialised with small positive and negative values, which are then left bit shifted by a small random amount (so that the result always fits into a machine word). mp++ integers with 1 limb of static size are employed.

2-limb unsigned integers

In this setup, the integer vector is initialised with non-negative values in the \(\left[2^{64},2^{128}\right)\) range, which are then left bit shifted by a small random amount (so that the result always fits into 2 machine words). mp++ integers with 2 limbs of static size are employed.

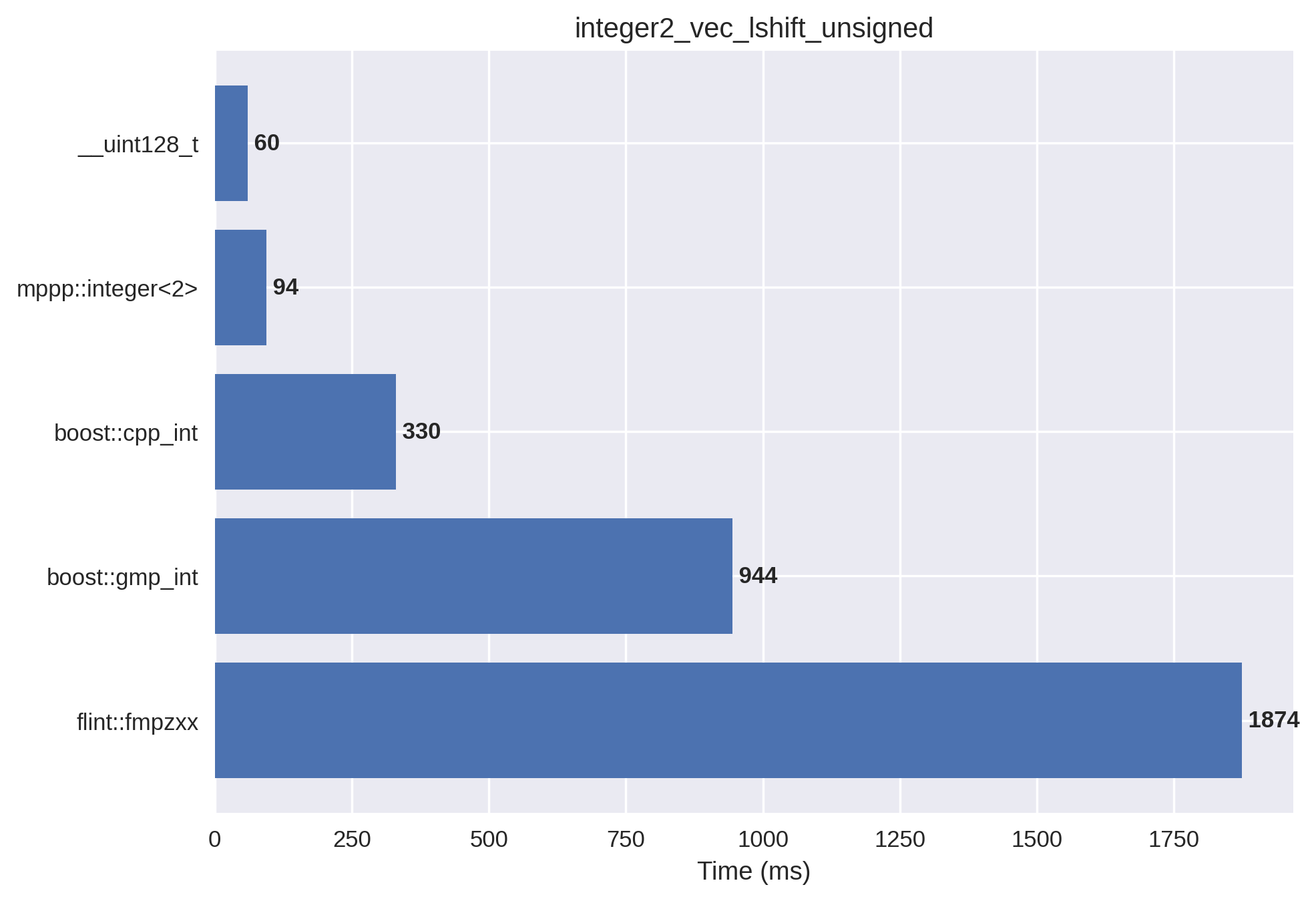
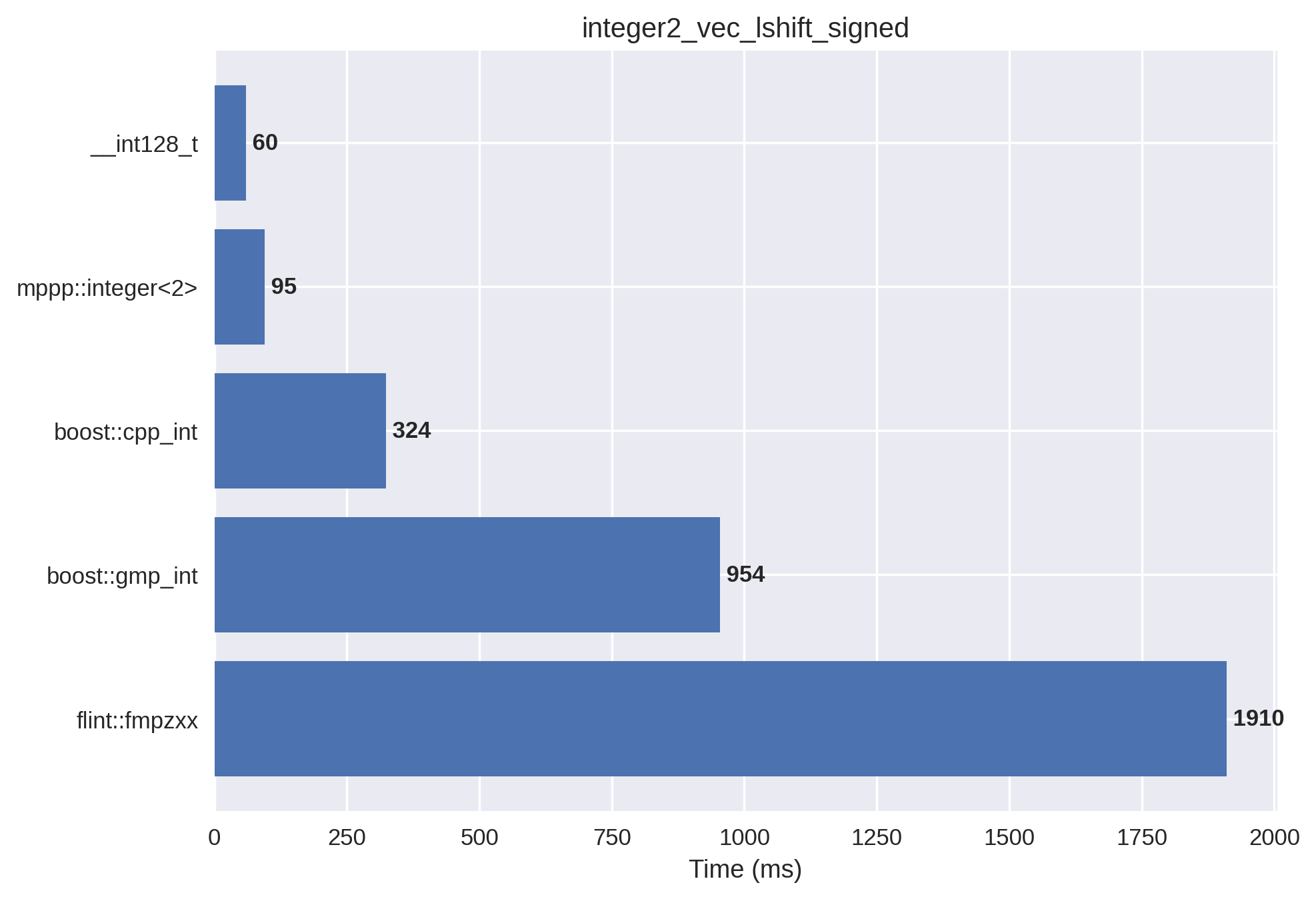
2-limb signed integers

In this setup, the integer vector is initialised with positive and negative values in the \(\left(-2^{128},2^{128}\right)\) range, which are then left bit shifted by a small random amount (so that the result always fits into 2 machine words). mp++ integers with 2 limbs of static size are employed.

GCD

In this benchmark we compute the element-wise GCD of two randomly-generated vectors of size \(3\times 10^7\), followed by the sum of all the values in the GCD vector.

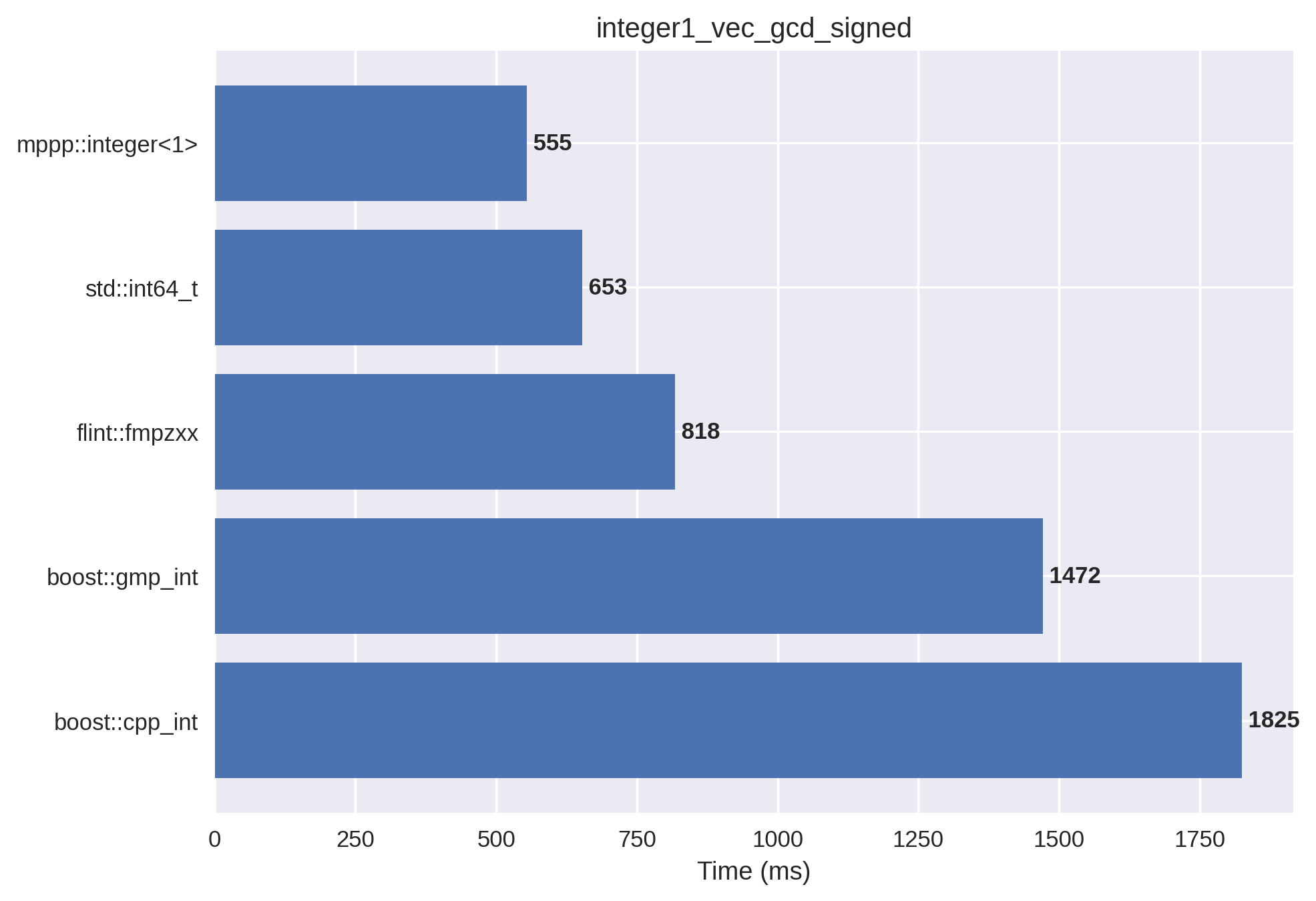
1-limb signed integers

In this setup, the vectors are initialised with small positive and negative values. All the computations fit within a single 64-bit word, and mp++ integers with 1 limb of static size are employed. For the computation of the GCD of std::int64_t values, the std::gcd() function from the C++17 standard library is employed.

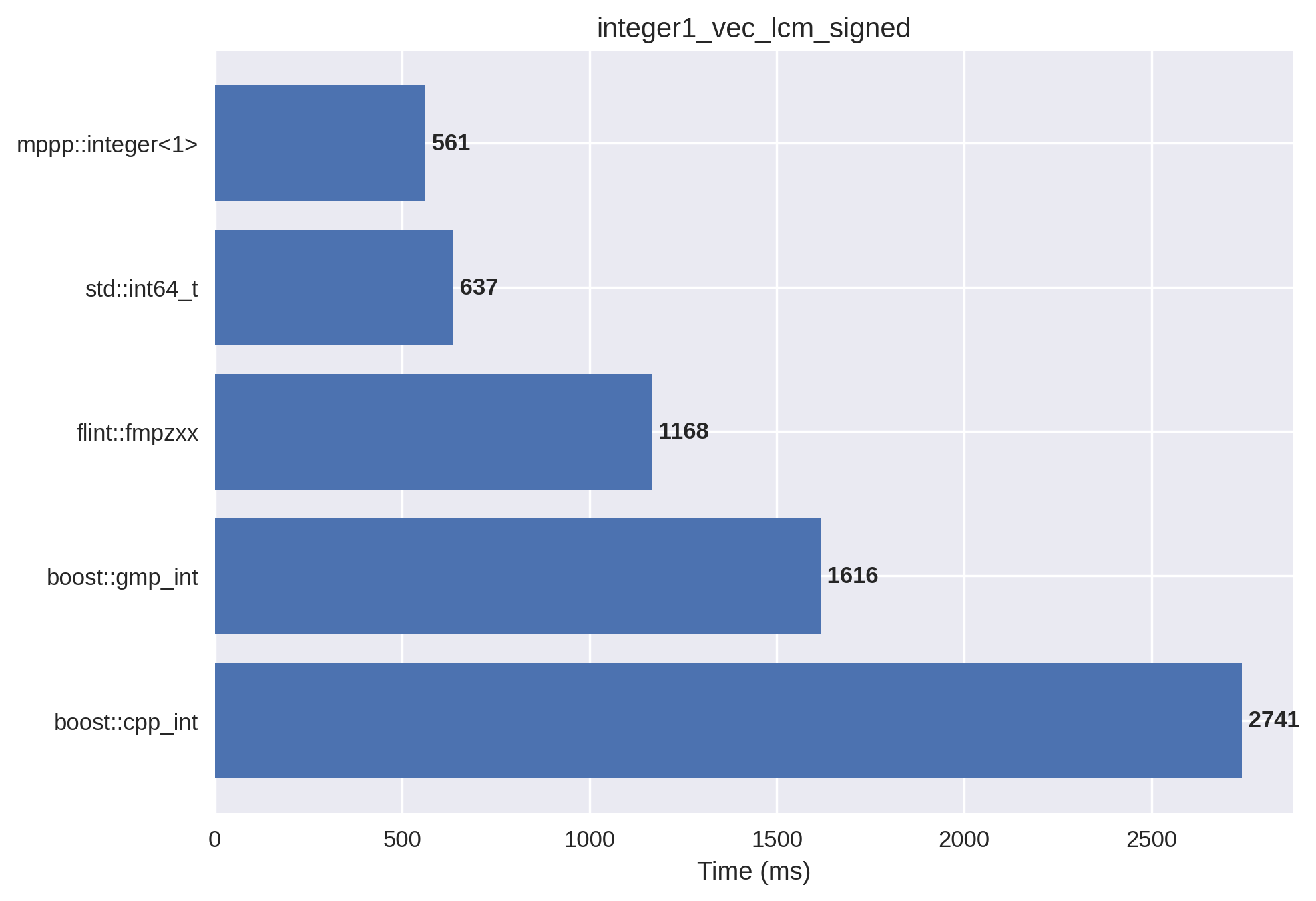
LCM

In this benchmark we compute the element-wise LCM of two randomly-generated vectors of size \(3\times 10^7\), followed by the sum of all the values in the LCM vector.

1-limb signed integers

In this setup, the vectors are initialised with small positive and negative values. All the computations fit within a single 64-bit word, and mp++ integers with 1 limb of static size are employed. For the computation of the LCM of std::int64_t values, the std::lcm() function from the C++17 standard library is employed.